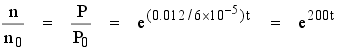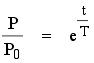Let us look into the time-dependent behaviour of a reactor following a change in k. First let us take a case in which k is much larger than 1. If k is the number of neutrons left after a completed cycle, then k - 1, or δk, is the number of extra neutrons per starting neutron. For n neutrons the gain each cycle is nδk. If the cycle time or neutron lifetime is l seconds, the gain in neutrons each second would be nδ/l. The result, in the form of an equation, for the rate of change of neutrons with time would be:

If at time zero there were n0 neutrons, at time t there would be:

The lifetime may be estimated from the thermal velocity, v, and the average distance a neutron travels along its path before being absorbed in fissionable material, λ_a = 1/Σ_a (as discussed before).

As an example, if the absorption mean free path, λ_a, is 13.2 cm and v is 2200 m/s then l = λ_a/v and l ≈ 6x10^-5s (60 μs). Now it may be seen how rapid the rise of the neutron level, and hence the power, can be for an excess reactivity (δk or ρ) of 0.012 or $1.71:

At the end of 0.01s, n/n₀ would rise to e² = 7.40; by 0.1s it would be e²⁰ = 4.85 x 10⁸; and in 1s it would become e²⁰⁰ = 7.23 x 10⁸⁶! This means that without delayed neutrons, the reactor response is very rapid. Clearly, a power increase of 2 x 10⁸⁶ in one second is difficult to control. When δk is ≥ β_eff, as in this example, the reactor is critical on prompt neutrons alone and is, therefore, said to be prompt critical. Uncontrolled prompt criticalities should obviously be avoided. However, with specially designed fuel like in the TRIGA reactors they are initiated deliberately in pulsing the reactor. An alternative convenient expression for the power change comes from the introduction of the reactor period T = l/δk.

The reactor period, T, is defined as that length of time required to change reactor power (or neutron density) by a factor of e. T is sometimes called the "e folding time", meaning that every T seconds of operation, n/n₀ increases by a factor e = 2.718. For the previous example, T is 0.005 s.

The estimates just made did not take into account the effect of delayed neutrons. About 0.7% (β_eff) of the 2.43 neutrons per fission are emitted by fission product decay, which come off statistically rather than instantaneously. The characteristic half-lives of the emitters are known, ranging from 0.23 to 55.7 s, as shown in Table 1. For values of δk less than 0.7% the average half-life of the emitters is the determining factor in the cycle lifetime rather than the time between thermalisation and absorption. For δkβ_eff, the delayed neutrons play their role in slowing down the cycle, and the neutron level rises much more slowly. A reactor that is operating in conjunction with a δkβ_eff is termed delayed critical because multiplication is based on both prompt and delayed neutrons.