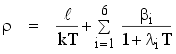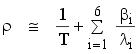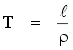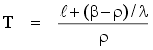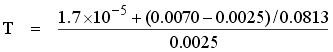The relationship between a step change in reactivity (ρ) and the resulting reactor period (T) allowing for the delayed neutrons, can be derived in the form of an equation such as:

This equation is often called the reactivity equation or the inhour equation, although strictly speaking this is not the inhour equation proper. (The term inhour comes from expressing reactivity in the units of inverse hours. The inhour unit is then that reactivity which will make the stable reactor period equal to one hour.) These are numerous different formulations of the reactivity equation, but this one will suffice for the purposes of this manual.

For a given reactor, the quantities β_i, λ_i, l, and k are known (often k ≈ 1 and is left out of the equation) so that the period can be determined when the reactivity is known and vice versa. This is best done numerically and then the results presented in tables or as a graph. Figure 11 shows the results of such calculations plotted for the TRIGA reactor for positive reactivities.

When the stable period is large (i.e., when the reactivity is very small), then unity may be neglected in comparison with λ_iT and l/kT is small compared to the summation term. The reactivity equation then reduces to

It can be seen that the reactivity is now independent of l, and is inversely proportional to the period for a given fuel. This explains why the curves on Figure 11 join together and have the shape they do for small reactivities.

For sufficiently large values of reactivity, the period is small, and the summation term of the reactivity equation can be neglected in comparison with the first term. The equation then becomes:

and the period is given by:

which is the same if all of the fission neutrons were prompt. This is shown in the top part of Figure 11 where the period is clearly dependent on the prompt neutron lifetime.

When the delayed neutrons are taken into account, the average neutron lifetime is increased considerably. Therefore, an effective lifetime (l_e) can be defined and approximated by:

And the stable period becomes

Using parameter values applicable to a typical TRIGA reactor and a reactivity change of 0.0025 ($0.357), the period can be calculated thus.

Using P/P₀ = e^t/T this means that in one second the power would increase by a factor of 1.05. This is much slower than that for δk = 0.012 when there is no effect from delayed neutrons. If it were not for delayed neutrons, reactors would be very difficult to control.

NOTE: It is important to realize that the inhour equation is only valid at low power levels where there are no temperature affects in progress. As the reactor power level increases and the negative temperature coefficient begins to exert its influence, the inhour equation will no longer hold true.